Съдържание
Изследването на характеристиките на триизмерните геометрични фигури се занимава със стереометрия. Една от добре познатите обемни фигури, които се появяват в геометричните задачи, е правата призма. В тази статия ще разгледаме какво представлява и ще опишем подробно призма с триъгълна основа.
Призма и нейните видове
Призмата се определя като фигура, образувана от успоредното преместване на многоъгълник в пространството. Тази геометрична операция дава фигура, състояща се от няколко паралелограма и два еднакви многоъгълника, успоредни един на друг. Паралелограмите са страните на призма, а многоъгълниците - нейните основи.
Всяка призма има n+2 страни, 3*n ръба и 2*n върха, където n е броят на ъглите или страните на многоъгълната основа. Изображението показва петоъгълна призма, която има 7 страни, 10 върха и 15 ръба.

Разглежданият клас фигури е представен с призми от няколко вида. Нека ги изброим накратко:
- вдлъбнати и изпъкнали;
- наклонени и прави;
- нередовни и редовни.
Всяка фигура принадлежи към един от следните три типа класификации. При решаването на геометрични задачи е най-лесно да се извърши изчисления за Правилни и правилни призми. Последното ще разгледаме по-подробно в следващите параграфи на статията.
Какво е права призма??
Вдлъбната или изпъкнала форма се нарича правоъгълник, Редовно или нередовно Призма, чиито всички страни са четириъгълници с ъгли 90°. Ако поне един от четириъгълниците на страните не е правоъгълник или квадрат, призмата се нарича наклонена призма. Може да се даде и друго определение: права призма е фигура от дадения клас, при която всеки страничен ръб е равен на височината. Височината h на една призма е разстоянието между основите ѝ.
И двете горепосочени определения, че това е права призма, са еднакви и самодостатъчни. От това следва, че всички диедрични ъгли между всяка от основите и всяка от страничните страни са 90°.
По-горе беше казано, че правите фигури са удобни за работа при решаване на задачи. това е така, защото височината е равна на дължината на страничния ръб. Последният факт улеснява изчисляването на обема на фигурата и площта на страничната ѝ повърхност.

Обем на права призма
Обемът е вътрешна стойност на всяка пространствена фигура, която в цифрово изражение представлява частта от пространството, заключена между повърхностите на въпросния обект. Обемът на една призма може да се изчисли по следната обща формула:
V = So*h.
Това означава, че произведението на височината по площта на основата ще даде желаната стойност V. Тъй като основите на права призма са равни, удобно е да се изчисли площта So всеки от тях може да бъде взет.
Предимството на използването на горната формула точно за права призма в сравнение с други призми е, че височината на фигурата се намира много лесно, тъй като съвпада с дължината на страничните ръбове.
Площ на страничната повърхност
Удобно е да се изчисли не само обемът на права фигура от въпросния клас, но и нейната странична повърхност. Всъщност всяка от страните му е или правоъгълник, или квадрат. Всеки ученик знае как да изчисли площта на тези плоски фигури; за целта съседните страни трябва да се умножат една по друга.
Да предположим, че в основата на призмата лежи произволен n-ъгълник, чиито страни са равни на ai. Индекс i е от 1 до n. Площта на един правоъгълник се изчислява по следния начин
Si = ai*h.
Странична повърхност Sb може лесно да се изчисли, като се съберат всички площи Si правоъгълници. След това получаваме окончателната формула за Sb на правоъгълна призма:
Sb = h*∑i=1n(ai) = h*Po.
Така, за да определите площта на страничната повърхност на правоъгълна призма, умножете височината ѝ по периметъра на едната основа.
Задача с триъгълна призма

Нека приемем, че дадената призма. База - правоъгълен триъгълник. Катетите на този триъгълник са 12 cm и 8 cm. Трябва да изчислим обема на фигурата и нейната обща площ, ако височината на призмата е 15 см.
Нека първо изчислим обема на права призма. Триъгълникът (правоъгълен) в основата си има площ:
So = a1*a2/2 = 12*8/2 = 48 см2.
Както може да се предположи, а1 и2 са катетите в това равенство. Знаейки площта на основата и височината (cm. (вж. условието на задачата), можем да използваме формулата за V
V = So*h = 48*15 = 720 cm3.
Общата площ на фигурата се формира от две части: площите на основите и страничната повърхност. Площите на две основи са равни:
S2o = 2*So = 48*2 = 96 см2.
За да изчислим площта на страничната повърхност, трябва да знаем периметъра на правоъгълния триъгълник. Нека да изчислим чрез Питагоровата теорема хипотенузата му a3, имаме:
a3 = √(a12 + a22) = √(122 + 82) = 14,42 cm.
Тогава периметърът на триъгълника на основата на права призма е
P = a1 + a2 + a3 = 12 + 8 + 14,42 = 34,42 cm.
Прилагане на формулата за Sb, която беше написана в предишната точка, получаваме:
Sb = h*P = 15*34,42 = 516,3 cm.
Чрез сумиране на площите S2o и Sb, получаваме общата площ на изследваната геометрична фигура:
S = S2o + Sb = 96 + 516,3 = 612,3 cm2.

Триъгълната призма, изработена от специални видове стъкло, се използва в оптиката за изследване на спектрите на обекти, излъчващи светлина. Такива призми са способни да разлагат светлината на съставните ѝ честоти благодарение на явлението дисперсия.
 Площ на повърхността на права призма: формули и примерна задача
Площ на повърхността на права призма: формули и примерна задача Геометрична фигура призма. Свойства, видове, формули за обем и площ. Правилна триъгълна призма
Геометрична фигура призма. Свойства, видове, формули за обем и площ. Правилна триъгълна призма Какво е права призма?? Формули за дължината на диагоналите, площта на повърхността и обема
Какво е права призма?? Формули за дължината на диагоналите, площта на повърхността и обема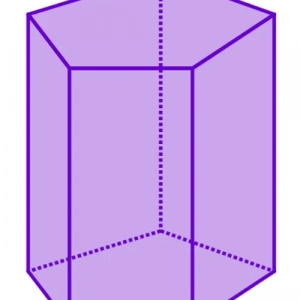 Какво е призма? Видове форми. Формули за обем и площ. Призма във физиката
Какво е призма? Видове форми. Формули за обем и площ. Призма във физиката Формула за обема на призма. Обеми на правилни четириъгълни и шестоъгълни фигури
Формула за обема на призма. Обеми на правилни четириъгълни и шестоъгълни фигури Как се определя площта на напречното сечение на цилиндър, конус, призма и пирамида? Формули
Как се определя площта на напречното сечение на цилиндър, конус, призма и пирамида? Формули Какво е тангенциално ускорение? Формули, примерна задача
Какво е тангенциално ускорение? Формули, примерна задача Идеален газ. Уравнението на клапейрон-менделеев. Формули и примерен проблем
Идеален газ. Уравнението на клапейрон-менделеев. Формули и примерен проблем Площ на пресечен конус. Формула и примерна задача
Площ на пресечен конус. Формула и примерна задача